

| How To Avoid Nearsightedness
|
Physical concepts are free creations of the human mind, and are not, however it may seem -- uniquely determined by the external world. In our endeavor to understand reality we are somewhat like a man trying to understand the mechanism of a closed watch. He sees the face and the moving hands, even hears it ticking, but he has no way of opening the case. If he is ingenious he may form some picture of the mechanism which could be responsible for all the things he observes, but he may never be quite sure his picture is the only one which could explain his observations. He will never be able to compare his picture the real mechanism and he cannot even imagine the possibility of the meaning of such a comparison. - Albert Einstein
In the previous chapter we developed a very accurate equation that duplicates the eye's behavior. The eye needs a very high level of tracking accuracy; using very basic data, we can estimate that the eye tracks its environment with a probable-error of better than 0.57 diopters.
Detailed measurements made by Dr. Francis Young show major changes in the optical components of the growing human and primate eye. Paradoxically, the eye maintains an over-all focal accuracy of better than one percent of its total power. The eye maintains this accuracy (relative to its visual environment) even though individual optical components are changing in an unpredictable manner.
Dr. Lawrence Stark's work has demonstrated high level accuracy for the accommodation (lens/retina) neurological system. This chapter extends his work by developing a perturbation (growth) control equation that accurately predicts the eye's response to step-change disturbances.
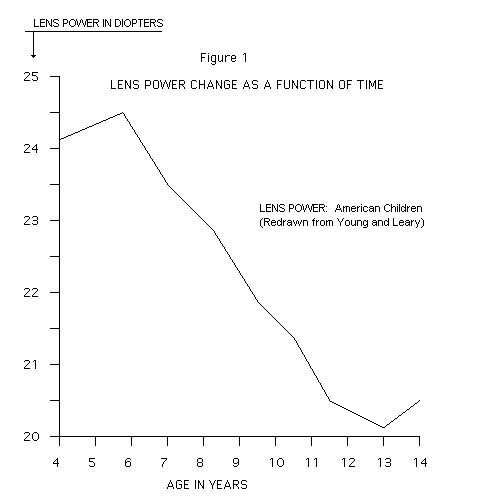
The lens of the human eye undergoes a focal power change of about 20 percent over a period of ten years. Without reference to feedback control concepts, a systems engineer will be hard pressed to explain focal accuracies of one percent for the normal eye, while major optical components are changing by 20 percent.
A graph of this focal change, and other optical parameter changes have been published by Dr. Francis Young and Dr. George A. Leary. (1) (See Figure 1)
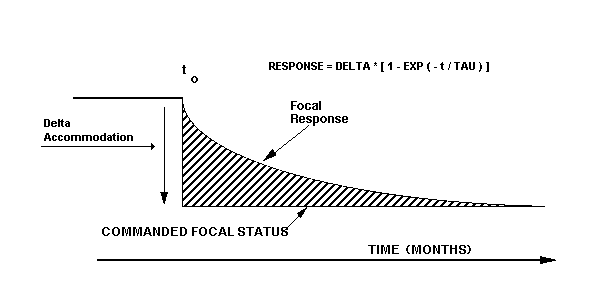
As previously developed, the transfer function for the long-term growth of the eye is: (2)
Where: TAU = 100 Days. (The eye's time-constant)
When a step-function is applied to this transfer function, the resulting equation is:
The time response of this function is: (3)
If a perturbation occurs within the control loop, it will cause not only a step-input to the system, but an immediate perturbation in the focal setting of the eye:
System's Response = [ Perturbation ] * [ 1 / ( TAU s + 1 ) ]
The standard response for an impulse perturbation is:
Focus = Offset + Accommodation - Perturbation * EXP ( - t / TAU )
Let's examine the equation as applied to wild monkey's eyes.
Perturbation = 0 diopters Offset = +1.5 diopters
Time = 300 days TAU = 100 Days
Accommodation (Average) = - 0.9 diopters
Focus = Offset + Accommodation - Perturbation * EXP ( - t / TAU )
Focus = 1.5 + ( -0.9 ) - ( 0 ) * EXP ( -300/100 )
Focus = + 0.6 Diopters
This result corresponds to +0.577 diopters mean value, obtained from measurements of a large number of wild (open-pen) monkey's normal eyes.
Now, consider the eye's response to a - 0.5 diopters change in the focal power of the cornea. (This change could be induced by use of a -0.5 diopter contact lens) Prior to the perturbation, the focal status was + 0.6 diopters. Immediately after the perturbation: (At t = 0 )
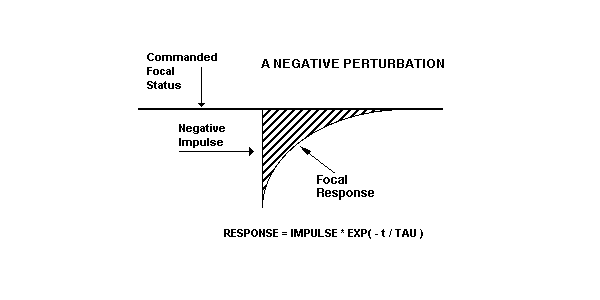
Focus = Offset + Accommodation - Perturbation * EXP ( - t / TAU )
Focus = 1.5 + (-.9) - (-.5) * EXP ( - 0 / 100 )
Focus = +1.1 diopters
After 300 days, the focal status will be:
Focus = 1.5 + (-.9) - (-.5) * EXP ( - 300 / 100 )
Focus = + 0.625 or approximately + 0.6 diopters
The eye's focal control system has returned the eye to the focal status that existed before the -0.5 diopter perturbation occurred.
In a similar vein, we can predict the eye's response to a + 0.5 diopter perturbation. (Simulated by use of a +0.5 diopter contact lens.)
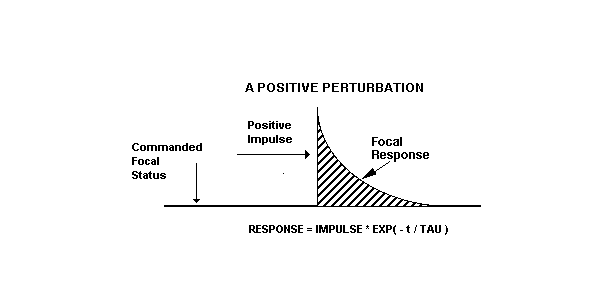
Focus = 1.5 + (-.9) - ( +.5) * EXP ( - 300 / 100 )
Focus = + 0.575 or approximately + 0.6 diopter
(If the +0.5 contact lens is now removed, the eye's focal status will be +1.0 diopters.)
Obviously, the human eye is not subject to only a single perturbation. We can, nevertheless, deduce the control action of the normal eye by studying the response of the eye to such idealized disturbances.
In actual fact, the eye is subject to continuous perturbations (noise) while growing. This noise tends to randomize the eyes' focal status. The control action of the normal eye works to overcome this randomness, exercising control over the appropriate optical components (corneal radius, length) to ensure accurate focus. A study of monkeys' eyes demonstrates that, with a steady state visual environment, their normal eyes maintain a focal accuracy of better than 1.0 percent.
The graph on the following page presents two computer-generated statistical distributions for wild, or "open pen" monkeys' eyes. The focal status histogram was obtained from measurements made by Dr. Young on 375 monkeys. The accommodation histogram is the estimated average value of accommodation for all the monkeys. Some monkeys will spend more time looking at close objects, and will have an average value of accommodation of perhaps - 1.2 diopters (and corresponding focal state of + 0.3 diopters), while other monkeys will spend more time looking at distant objects and will have an average value of accommodation of perhaps - 0.6 diopters (and a corresponding focal state of + 1.1 diopters). The preliminary mean value for the 375 monkeys is -0.9 diopters (producing an over-all focal status of +0.6 diopters.) (See Figure 2)
If the normal primate eye is to achieve a high level of focal accuracy in the presence of continuous perturbations, the author has concluded that the eye must employ dynamic control to set its focus. This chapter presents a high performance model that provides a focal control mechanism that is, as far as we can determine, consistent with all the physical evidence pertaining to the normal eye's behavior.
The model evolved as a result of a long investigation in which many preliminary approaches were discarded because they led to inconsistencies. It is clear that the number of approaches that can satisfy the evidence is limited. An electrical engineer, when faced with similar engineering requirements for focal precision, will develop this type of design to meet the accuracy requirements of the eye.
The philosophy of this chapter has been to study the focal control process of the normal eye by treating it as a design problem. The procedure followed is to develop a system model with the focal performance capability comparable to the normal primate eye.
Measurements on individual optical components of the eye are exacting, and it is difficult to say which optical component causes a specific problem. The researcher can be aided by an engineering approach to this complex system, since the eye is an intricate data-processing system. The primary neurological process is controlling a dynamic (100 day time-constant) focal system on a microscopic level.
It should be remembered that there are several major optical components of focus, any of which can dramatically affect the focal state of the normal human eye. While the eye is growing, these components are continually changing in value.
Figure 2
Histograms for the Average Accommodation Status
and the Focal Status of the Normal Eye
DIOP FOCAL ACCOM
TERS STATUS MODATE ESTIMATED ACCOMMODATION STATUS -- PERCENT
.0 2.0 4.0 6.0 8.0 10.0 12.0 14.0 16.0 18.0 20.0
....................................................
-1.5 .0 .2 .
-1.4 .0 .9 . A
-1.3 .1 2.7 . A
-1.2 .1 6.5 . A <---------------<< Accommodation
-1.1 .2 12.1 .F A
-1.0 .3 17.6 .F A
-.9 .4 20.0 . F A<---
-.8 .6 17.6 . F A V
-.7 .8 12.1 . F A V
-.6 1.1 6.5 . F A |
-.5 1.4 2.7 . F |
-.4 1.8 .9 . A F |
-.3 2.3 .2 . F Offset 1.5 Diopters >>-->|
-.2 2.9 .0 . F |
-.1 3.4 .0 . F |
.0 4.0 .0 . F |
.1 4.6 .0 . F |
.2 5.1 .0 . F |
.3 5.6 .0 . F |
.4 6.0 .0 . F |
.5 6.2 .0 . F v
.6 6.3 .0 . F<-------------------
.7 6.2 .0 . F
.8 6.0 .0 . F
.9 5.6 .0 . F
1.0 5.1 .0 . F
1.1 4.6 .0 . F
1.2 4.0 .0 . F
1.3 3.4 .0 . F<----------------<< Focal Status
1.4 2.9 .0 . F
1.5 2.3 .0 . F
1.6 1.8 .0 . F
1.7 1.4 .0 . F
1.8 1.1 .0 . F
1.9 .8 .0 . F
2.0 .6 .0 . F
...................................................
.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0
MEASURED FOCAL STATUS -- PERCENT
When a physiologist experiments on this complicated data processing operation, he is in the same position as a technician who is presented with a computer system that determines rocket guidance. He is then told to make measurements on the individual components of the device until he determines which component establishes the tracking accuracy of the system. Actually, the physiologist is in a more difficult position because so much of the data processing of the eye is at the molecular level, almost beyond the reach of his instruments.
The mathematical systems concepts used in automatic control evolved out of necessity, as it became apparent that modern servo systems could not be understood by studying the characteristics of their individual components. This truth applies just as strongly to complex processes encountered in biological-optical systems. The electronics engineer can establish a solid mathematical foundation for an analysis that will accurately predict the normal eye's focal control response.
The same equation that precisely anticipates the normal eye's perturbation control also predicts that nearsightedness can be avoided. In addition, the equation can give conceptual and practical guidance to a successful nearsightedness avoidance effort.
There are other more sophisticated means of determining the eye's tracking accuracy, and these techniques will be developed in the next chapter.
Focal Accuracy: The eye is about 2.4 cm in length. The eye must have a focal power of 57 diopters to focus light on the retina. The focal status histogram for normal eyes has a standard deviation of .843 diopters, and a probable error of .843 X .674 = .568 diopters. We may, therefore, specify that the eye has a tracking probable error of .568/57 or approximately one percent of its total focal power. This is the worst-case value. For a number of reasons, we should expect that the tracking accuracy of the normal eye will be considerably better than one percent. In the next chapter we will provide an analysis that demonstrates that the actual tracking probable-error is on the order of 1/10 diopters.
1. Young, F., Leary, G. VISUAL CHARACTERISTICS OF APES AND PERSONS (207-225) Progress in Ape Research (1977)
2. Brown, O., Berger, R. A NEARSIGHTEDNESS COMPUTER (343-346) Proceedings of the 7th New England Bioengineering Conference (1979)
3. Brown, O., Young, F. PHYSIOLOGICAL MODELING: THE LONG-TERM GROWTH OF THE EYE Proceedings of the 8th New England Bioengineering Conference (1980)