

| How To Avoid Nearsightedness
|
Science is the attempt to make the chaotic diversity of our sense-experience correspond to a logically uniform system of thought. - Albert Einstein
It is important that we conduct a thought experiment before we commit ourselves to doing a full scale measurement study of the normal eye's behavior. If the eye is identified as normal, we can then presume that it is continuously adjusting its long-term focus by a dynamic control process.
We will exclude the defective eye from the present analysis. In this chapter I will present a conceptual scheme for the normal eye's behavior and in the next chapter the actual factual data that confirms this specific behavior of the normal eye. The equation developed from this analysis is an order of magnitude more accurate than the Helmholtz-heredity theory in its power to predict experimental results.
The short-term (accommodation) control of the eye is accurate and effective. It is likely that this (averaged) signal is made available to the long-term growth control of the eye for correct positioning of the retina relative to the accommodation system. This is the thesis of this presentation. (1) A feedback control circuit will insure that the retina is adjusted to the average visual environment of the eye. (Figure 1) The Laplace transform of the eye's growth control system is:
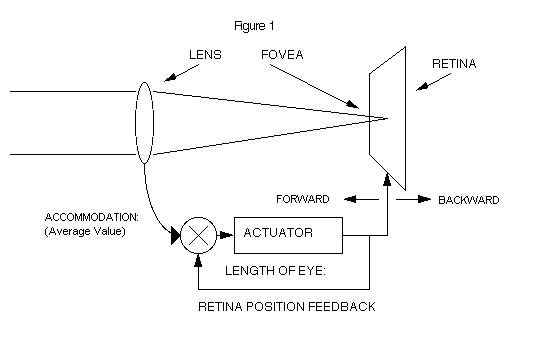 |
| The Eye's Focal Setting is Controlled by a Long Time-Constant Positioning Servo with a Physiological Offset of 1.5 Diopters |
| Focus = | The focal state of the normal eye. |
| Offset = | The difference between the average value of accommodation and the focal state of the normal eye -- considered over a period of months. (For a population of normal eyes the value is +1.5 diopters.) |
| Accommo- dation = | Normal accommodation. By design, the accommodation system's focal state is almost an exact replica of the visual environment. The system is blur-driven and has a time-constant of about 1/4 of a second. |
| Step- Input = | The step-input represents a sharp quantitative change in the average value of accommodation. |
| EXP = | Exponential function. |
| e - t / TAU = | EXP ( - t / TAU ) |
| e = | 2.718 |
| t = | Time, in days after the step change is induced in the average visual environment. |
| TAU = | The time-constant of a normal eye. All normal eyes have a time-constant. (The typical value for the normal eye is 100 days) |
Does this equation represent the fundamental long-term focal behavior of the normal eye? Only a direct factual test will confirm the accuracy of this equation. To verify this, we will subject the human eye to a fundamental experiment.
The primary technique for the evaluation of two theories in science is to compare their predictive capabilities. The theories must be stated in mathematical terms, and must yield quantitative predictions. Both the Helmholtz-passive and Helmholtz-dynamic theory of the normal eye's behavior meet this requirement. Both theories yield explicit numerical predictions that can be checked against reality by actual test. The theory that yields the most accurate prediction becomes the controlling theory, and will be relied on for further analysis.
The first question is this: Does the equation predict the focal control characteristic of the normal human eye; day after day, year after year? Using 231 days as the value for time, and - 0.9 diopters (estimated) as the average value of accommodation, we find that the normal eye sets its long-term focus to + 0.6 diopters. Actual measurement of monkeys shows that their eyes have a focal status of + 0.57 diopters when their eyes are maintained in an open visual environment. (2) The transfer function correctly describes and predicts this dynamic behavior characteristic of the normal eye in an open environment. This is the first test of any theory that characterizes the normal eye's long-term behavior.
If we can make a sudden shift in the eye's visual input, we can check the difference between these two theories of the eye's long-term behavior. A negative lens may be used to achieve this goal.
The negative lens causes parallel rays of light (from infinity) to be diverged, causing the accommodation mechanism to adjust as though the object is much closer. All objects closer than infinity will be moved correspondingly closer to the eye. (Figure 2)
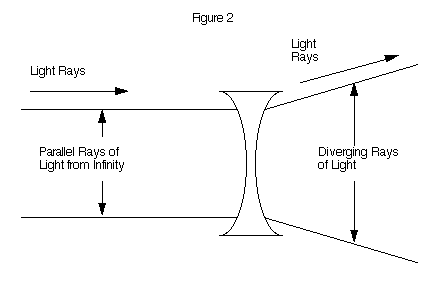 |
| A Negative Lens Constitutes a Step Input for the Eye |
In order to test these two Helmholtz theories of vision we will subject them to a hypothetical test. We will select 100 children (eight years of age) and verify that they have normal vision. (A positive focal state of + 0.6 diopters.)
Fifty of these children will wear a - 1.2 diopter lens (33 inch focal length). The other fifty children will be the control group. The focal state of the normal eye will be measured at seven day intervals. A FORTRAN generated graph, using the numerical predictions of the Helmholtz-passive and Helmholtz-dynamic theories are shown in figure 3.
The "delta" accommodation is zero diopters for the control group.
Focus = Offset + Accommodation + Delta * [ 1 - EXP ( -t / TAU ) ]
Focus = ( 1.5 D ) + ( - 0.9 ) + ( 0 ) * [ 1 - EXP ( - 231 / 100 ) ]
Focus = + 0.60 Diopters, after 231 Days.
The "delta" accommodation is - 1.2 diopters for the test group.
Focus = ( 1.5 ) + ( - 0.9 ) + ( -1.2 ) * [ 1 - EXP ( - 231 / 100 ) ]
Focus = - 0.48 Diopters, after 231 Days.
PREDICTED STEP CHANGE = -1.2 D
FOCAL TIME CONSTANT = 100 DAYS
STATUS: F = FEEDBACK H = HEREDITY L = STEP INPUT
DAYS FEED HERE-
INTO BACK DITY
TEST DIOPTERS NEARSIGHTED POSITIVE FOCUS
-1.0 -.8 -.6 -.4 -.2 .0 .2 .4 .6
---- ---- ---- .........................................
0 .60 .60 L <-----------------------<< F
7 .52 .60 L Step Change 1.2 D F H
14 .44 .60 L (Negative Lens) F H
21 .37 .60 L . F H
28 .31 .60 L . F H
35 .25 .60 L . F H
42 .19 .60 L . F H
49 .14 .60 L . F H
56 .09 .60 L . F H
63 .04 .60 L .F H
70 .00 .60 L F H
77 -.04 .60 L F. H
84 -.08 .60 L F . H
91 -.12 .60 L F . H
98 -.15 .60 L F . H
105 -.18 .60 L F . H
112 -.21 .60 L F . H
119 -.23 .60 L F . H
126 -.26 .60 L F <-----<< Test H
133 -.28 .60 L F . Group H
140 -.30 .60 L F . H
147 -.32 .60 L F . H
154 -.34 .60 L F . H
161 -.36 .60 L F . H
168 -.38 .60 L F . H
175 -.39 .60 L F . H
182 -.41 .60 L F . H
189 -.42 .60 L F Control >>--------> H
196 -.43 .60 L F Group . H
203 -.44 .60 L F . H
210 -.45 .60 L F . H
217 -.46 .60 L F . H
224 -.47 .60 L F . H
231 -.48 .60 L F . H
........................................
-1.0 -.8 -.6 -.4 -.2 .0 .2 .4 .6
Actual testing will help us choose between these two concepts of the normal eye's behavior. If the test group does not show a change in its focal state, the passive theory of the normal eye's behavior will be confirmed. If the test group demonstrates a change, the dynamic concept for the normal eye's behavior will be confirmed.
After 231 days the conceptual test of the normal eye's behavior was terminated. The test need not be carried to this extent to demonstrate the greater predictive accuracy of the dynamic theory. Since the heredity of the control group is identical to the heredity of the test group, both groups should continue to maintain their positive focal state, if the Helmholtz-passive theory is correct.
In this thought experiment, the fifty children who wore a -1.2 diopter lens have undergone a -1.14 diopter net change in their normal eye's focal state, while the control group continues to maintain their + 0.6 diopter focal state. The conclusion is that the Helmholtz-dynamic theory is an order of magnitude more accurate than the heredity theory in representing the fundamental behavior characteristic of the normal eye.
The Helmholtz-dynamic theory leads to an exact mathematical analysis and representation of the performance of the eye. (3) The Helmholtz-heredity theory produces inaccurate predictions about the long-term behavior of the normal eye.
There is a logical continuum between an accommodation (feedback) control system and a long-term focusing (feedback) system. There is a sharp logical break between a precisely accurate accommodation system and a Helmholtz-heredity theory of the normal eye's behavior.
1. Brown, O., Berger, R. A NEARSIGHTEDNESS COMPUTER, (343-346) Proceedings of the 7th New England Bioengineering Conference (1979) (Additional references can be found in this paper.)
2. Young, F. A. Unpublished study of 375 monkeys who were maintained in an open visual environment. Their mean focal status was +0.577 diopters.
3. Biernson, G. A FEEDBACK-CONTROL MODEL OF HUMAN VISION, Proceedings of the IEEE, Vol. 54 #6, (858-872) June, 1966